Smooth structure

In mathematics, a smooth structure on a topological manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform parts of differential calculus on the manifold. It is a special case of differential structure.

Contents

Definition

Maximal smooth atlas

Let M be topological n-manifold. A smooth atlas A on M is an atlas such that a transition map between any two coordinate charts contained in A is a C∞-diffeomorphism in 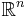\mathbb{R}^n. That is, every transition map is smooth in standard meaning and has a smooth inverse.

A smooth atlas is maximal when it is not contained in any strictly larger smooth atlas.

Smooth structure

A smooth structure on n-dimensional topological manifold is a maximal smooth atlas.

Discussion

By taking the union of all smoothly compatible atlases, we obtain a maximal smooth atlas. So this atlas contains every chart that is compatible with the smooth structure. There is a natural one to one correspondence between smooth structures and maximal smooth atlases. Thus, we may regard a smooth structure as a maximal atlas and vice versa.

In general, computations with the maximal atlas of a manifold are rather unwieldy. For most applications, it suffices to choose a smaller atlas. For example, if the manifold is compact, then one can find an atlas with only finitely many charts. When we are given some atlas smaller than maximal one, we know it is part of some unique maximal atlas.[1]

Confusion about terminology

Technicaly, we can put many distinct smooth structures on given topological manifold, therefore creating many distinct smooth manifolds.

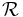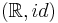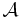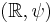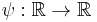For example, lets have two different smooth manifolds. First manifold \mathcal{R} is given as (\mathbb{R}, id), while the second one \mathcal{A} is (\mathbb{R}, \psi), where \psi: \mathbb{R}\to\mathbb{R} is given by 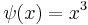\psi(x) = x^3. It is trivial to check that a transition map 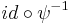id\circ\psi^{-1} is not smooth, so these two functions cannot be in the same smooth atlas.

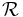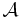So far so fine, we can say that \mathcal{R} and \mathcal{A} have different smooth structure and are different smooth manifolds. However, these two manifolds are diffeomorphic by map 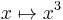x \mapsto x^3, so many authors consider these two manifolds as the same.

There exist, however, smooth manifolds with the same underlying topological manifold and different smooth structure that are really different, in the sense there does not exist diffeomorphism between them(see below). In other words, smooth manifolds that are diffeomorphic are can be considered as the same, while those that are merely Homeomorphic are different. Examples of manifolds that are "essentialy different" are exotic 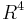R^4 and exotic sphere.

Also, some authors say smooth (map, structure, manifold) when they mean differential (map, structure, manifold) while others use it vice versa.

Exotic spheres

John Milnor showed in 1956 that the 7-dimensional sphere admits a smooth structure that is distinct from the standard smooth structure. A sphere equipped with a nonstandard smooth structure is called an exotic sphere.

Related structures

The smoothness requirements on the transition functions can be weakened, so that we only require the transition maps to be k-times continuously differentiable; or strengthened, so that we require the transition maps to real-analytic. Accordingly, this gives a 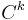C^k or (real-)analytic structure on the manifold rather than a smooth one. Similarly, we can define a complex structure by requiring the transition maps to be holomorphic.

See also

Differential structure, a generalization of smooth structure.

References

  1. ^ See Lee, Lemma 1.10
  • Lee, John M. (2006). Introduction to Smooth Manifolds. Springer-Verlag. ISBN 978-0-387-95448-6. 
  • Sepanski, Mark R. (2007). Compact Lie Groups. Springer-Verlag. ISBN 978-0-387-30263-8.